Electric Potential Of A Dipole

Electric Field and Potential Energy of an Electrical Dipole

An electric dipole is a pair of charges having equal magnitudes but opposite sign separated at a distance, say $d$. When such a dipole is placed in a uniform electrical field, the electric field exerts strength on the dipole which and then rotates the dipole in clockwise or anticlockwise management. Here nosotros hash out the electric field and potential energy of an electrical dipole.

Electric Field of a Dipole Equidistant from both Charges

Here we make up one's mind the electric field of an electric dipole. Consider a positive and a negative charges having equal magnitudes separated at a distance $d$. Such arrangement of charges is chosen an electric dipole. It's a good idea to commencement with a coordinate system equally shown in Figure ane.

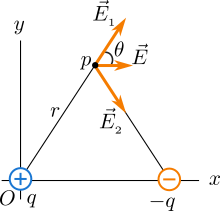
Effigy 1 The electric field of an electrical dipole at bespeak $p$ equidistant from both charges.

At present nosotros decide the electrical field at any signal $p$ which is located at the same distance $r$ from both charges. Both charges accept the same magnitude then the electric field magnitude at the point $p$ is also the same which is

\[E = k\frac{q}{{{r^two}}}\]

The y-component of electric field due to the electric dipole is a zilch vector, that is the y-component of one charge is equal in magnitude and contrary in direction to the y-component of another charge. The y-component of $\vec E_1$ due to positive charge is $Eastward \sin \theta \hat j$ and the y-component of $\vec E_2$ due to negative charge is $-E \sin \theta \chapeau j$, then they cancel each other. Here the unit vector $\hat j$ is the unit vector along y-axis. Both x-components of electric fields due to the electric dipole lie along the same line (parallel to x-axis) in the same direction and therefore the electric field at the bespeak $p$ is simply due to the 10-components of electrical fields of both charges.

The 10-component of electric field due to one charge is $E_x = E \cos \theta$ which is equal in both magnitude and direction to the ten-component of electrical field of another charge. Then the total electrical filed at the point $p$ is twice the x-component of electric field due to one charge that is, $E = 2E_x = 2E \cos \theta$. You know the electrical field magnitude $E$ from the above equation and therefore, the full electric field is

\[E = k\frac{2q \cos \theta}{r^2} \tag{1} \label{1}\]

In vector form if the unit vector towards x-direction is $\lid i$, the above equation is

\[\vec E = k{\frac{2q \cos \theta}{r^2}} \hat i \tag{2} \label{2}\]

Electric Field of an Electric Dipole on its Centrality

Now we detect the electric field of an electrical dipole at a point on the axis joining the 2 charges. The Effigy ii shows that the center of our coordinate organisation is the centre of the dipole. We are going to find the electric field at the point $p$ shown in Figure 2.

Figure 2 The electrical field at a point on the axis joining the two charges.

It's quiet simple that you need to add the electric fields due to both charges at the point. Consider that the electric field due to positive accuse is $\vec E_1$ and the electric field due to negative charge is $\vec E_2$. In an electric dipole the magnitude of both charges is the same say $q$ and are separated by a distance $d$. Therefore, the distance of positive charge from the betoken is $y + d/2$ and the distance of negative charge from the point is $y - d/ii$. Notation that the 10-components of electric fields due to both charges is nil. The electric field vectors $\vec E_1$ and $\vec E_2$ are

\[{\vec E_1} = k\frac{q}{{{{\left( {y + \frac{d}{two}} \right)}^2}}} \hat j\]

\[{\vec E_2} = -thousand\frac{q}{{{{\left( {y - \frac{d}{2}} \right)}^2}}} \hat j\]

The unit vector $\hat j$ gives the direction to the electric field vector which is along y-axis. If $E_{1y}$ is the y-component of $E_1$ and $E_{2y}$ is the y-component of $E_2$, so you know that $E_1 = E_{1y}$ and $E_2 = E_{2y}$ (there is no x-component of electric field at the point $p$). The net electrical field which is $\vec E = \vec E_y$ (the subscript y-represents the y-component) at the point $p$ is

\[\begin{align*} \vec East &= one thousand\left[ {\frac{q}{{{{\left( {y + \frac{d}{2}} \right)}^two}}} - \frac{q}{{{{\left( {y - \frac{d}{2}} \correct)}^two}}}} \correct]\widehat j\\ {\rm{or,}}\quad \vec E &= k\frac{q}{{{y^2}}}\left[ {{{\left( {1 + \frac{d}{{2y}}} \right)}^{ - two}} - {{\left( {1 - \frac{d}{{2y}}} \right)}^{ - 2}}} \right]\widehat j \end{align*}\]

Note that in an approximation that $y$ is much larger than $d$, the term obviously $\left| \frac{d}{2y} \correct| < 1$. Now we utilize the binomial expansion to solve the terms ${\left( {one - \frac{d}{{2y}}} \right)^{ - ii}}$ and ${\left( {ane + \frac{d}{{2y}}} \right)^{ - ii}}$. Note that the expression for the binomial expansion of ${(1 + 10)^n}$ when $\left| x \right|<ane$ is ${{(1+x)}^{n}}=1+nx+n(n-1)\frac{{{x}^{ii}}}{2}+...$. So,

\[\begin{marshal*} {\left( {1 - \frac{d}{{2y}}} \right)^{ - two}} &= 1 + \frac{d}{y} + \frac{3}{4}\left( {\frac{{{d^2}}}{{{y^2}}}} \right) + ...\\ {\rm{and,}}\quad {\left( {1 + \frac{d}{{2y}}} \correct)^{ - ii}} &= one - \frac{d}{y} + \frac{three}{iv}\left( {\frac{{{d^ii}}}{{{y^2}}}} \right) + ... \cease{align*}\]

Now keeping but the first two terms neglecting the smaller terms we have ${\left( {i - \frac{d}{{2y}}} \right)^{ - 2}} \cong 1 + \frac{d}{y}$ and ${\left( {i + \frac{d}{{2y}}} \correct)^{ - 2}} \cong 1 - \frac{d}{y}$. And so the net electric field is,

\[\brainstorm{marshal*} \vec E &= chiliad\frac{q}{{{y^ii}}}\left[ {\left( {one - \frac{d}{y}} \right) - \left( {one + \frac{d}{y}} \right)} \correct]\hat j\\ &= - thou\frac{{2qd}}{{{y^three}}}\lid j = - k\frac{{2p}}{{{y^3}}}\hat j = k\frac{{2\vec p}}{{{y^iii}}} \tag{3} \label{three} \end{marshal*}\]

As you can see from the to a higher place expression of the net electric field that the electric field is proportional to $\frac{1}{{{y^3}}}$ instead of $\frac{1}{{{y}^{2}}}$. The above expression of net electrical field tells us that the net electric field is forth negative y-direction in our instance shown in Figure 2. If you consider only the magnitude of the internet electric field, it is

\[E = k\frac{2p}{y^3} \tag{4} \label{4}\]

Potential Energy of an Electric Dipole

Here we find the potential free energy of an electric dipole in a uniform electrical field. Consider that the dipole is inside a compatible electric field equally shown in Figure 3. The two charges of the dipole are separated at a altitude $d$. The dipole makes an angle $\theta $ with the management of electric field. The electric field exerts force on each charge of the dipole. So the torque produced tends to rotate the dipole in anticlockwise direction.

Figure 3 The torque due to the electric field rotates the dipole to minimize its potential energy.

The force on negative charge is $F_1$ and on positive accuse is $F_2$. The magnitude of force on each charge is the same. Let the magnitude of 1 charge is $q$ and therefore the magnitude of strength on each charge is $F = qE$ where $Due east$ is the electrical field magnitude. The perpendicular altitude between the line of action of forces (shown in dotted line in Effigy 3) is $d\sin \theta $ so the lever arm for each strength is the same which is $\frac{d}{ii}\sin \theta $. The magnitude of torque $\tau $ for each charge is also the same which is $(qE)\left( \frac{d}{2}\sin \theta \right)$. Since both torques tend to rotate the dipole in anticlockwise direction, the net torque magnitude on the dipole is twice the torque magnitude on one of the charges which is:

\[\tau = qdE\sin \theta {\rm{ }} \tag{5} \characterization{5}\]

The product $qd$ is another physical quantity called electric dipole moment. The electrical dipole moment $\vec{p}$ has a management from negative charge to positive charge in an electric dipole. Now in terms of the electric dipole moment, the above expression can be written as

\[\tau = pE\sin \theta \tag{6} \characterization{6}\]

This is the expression for the cross product of vectors, and then in vector form it is $\vec{\tau }=\vec p \times \vec E$. You need to know the right paw thumb rule of vector product to know the direction of $\vec \tau$; the curved fingers requite the direction of rotation and the pollex gives the direction of $\vec \tau$ which in this example is perpendicularly towards you. As you lot tin can see in Effigy iii and from above equation the torque is nothing when $\theta $ is aught or $\pi $. When $\theta =0$, $\vec p$ and $\vec Eastward$ are antiparallel which is the position of unstable equilibrium. When $\theta =\pi $, $\vec p$ and $\vec E$ are parallel which is the position of stable equilibrium. And the torque always tends to rotate the dipole in stable equilibrium position.

At present let the torque rotates the dipole through a small angle $d\theta $ , then the pocket-size work washed past the torque is $dW=\tau d\theta $. Since the torque rotates the dipole in anticlockwise management, that is in the direction of increasing $\theta $ the work done is positive. The total work done by the torque is obtained past integrating $dW$ between limits $\theta_1$ and $\theta_2$:

\[Due west = \int\limits_{{\theta _1}}^{{\theta _2}} {\tau d\theta } = pE\int\limits_{{\theta _1}}^{{\theta _2}} {\sin \theta {\mkern 1mu} d\theta } = pE( - cos{\theta _2} + cos{\theta _1})\]

\[{\rm{or,}}\quad W = pE\cos {\theta _1} - pE\cos {\theta _2} \tag{7} \label{seven}\]

In the in a higher place equation Eq. \eqref{seven}, the quantity $pE \cos \theta$ is the potential energy of the electric dipole. It is denoted by $U$ and therefore, $U_1 = pE \cos \theta_1$ and $U_2 = pE \cos \theta_2$. So, $W=U_1 - U_2 = -(U_2 - U_1) = -\Delta U$. Therefore piece of work done is the negative of change in potential energy. You know from the conservation of mechanical energy that the piece of work done past gravitational force is likewise the negative of alter in gravitational potential free energy. The potential energy of the electric dipole is

\[U = pE \cos \theta \label{8} \tag{8}\]

In anticlockwise management $\theta $ increases and the potential energy goes on decreasing until becomes minimum in stable equilibrium position at $\theta = \pi$. At $\theta = \pi$, the potential energy is $U = -pE$ which is the most negative value. In anticlockwise direction the work done is positive; final potential energy is smaller than initial potential energy ($U_2 < U_1$) and the negative of change in potential energy is positive. Similarly in clockwise direction that is in the direction of decreasing $\theta $ the work done is negative; final potential free energy is greater than initial ($U_2 > U_1$) and the negative of change in potential free energy is negative. Annotation that the torque tends to minimize the potential energy of the dipole towards stable equilibrium position. At $\theta = 0$ the potential energy is maximum which is $U = pE$ and zippo at $\theta = \pi /two$. Note that zero potential energy does non hateful that the the dipole does not have potential free energy but you know that nil is greater than negative values.

If the torque rotates the dipole in clockwise management (the electric field management should be exactly reverse to the direction shown in Figure 3) which is in the direction of decreasing $\theta $, the work done should be positive (the torque is in the same direction of rotation). In this instance the final potential free energy is greater than initial and therefore the potential energy of the dipole is $U=-pE\cos \theta $.