Area Of A Segment Calculator

The Area of an Arc Segment of a Circle formula, A = ½• r²• (θ - sin(θ)), computes the area divers by 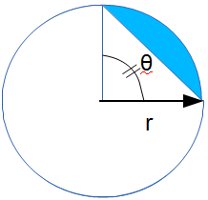/attachments/452e1b50-9dd6-11e3-9cd9-bc764e2038f2/CircSegCord.jpg A = f(r,θ) A = f(r,h) an arc and the chord connecting the ends of the arc (run across blue area of diagram).

INSTRUCTIONS: Choose units and enter the following:

(r) - This is the radius of the circle.
(θ) - This is the bending defining the arc.

Area of an Arc Segment of a Circle (A): The computer returns the area (A) in square meters. However the user can automatically convert the output units to numerous other uniform units via the pull-down carte.

Related Calculators

A = f(r,h) - Compute the area of an Arc Segment of a Circle based on the radius (r) and depth (h)

The Math / Science

If θ is unknown, the same area tin can be calculated if the depth (h) from the edge of the circle toward the heart is known. (See effigy) The following equation calculates the area using r and h: (Click on formula for solver)

`A=one/two * r^2 * (2 cos^-one((r-h)/r)- sin(2 cos^-1((r-h)/r))`
Circumvolve PARTS /attachments/452e1b50-9dd6-11e3-9cd9-bc764e2038f2/CircleStack.png
For the expanse of unlike parts or segments of a circumvolve, the following calculators will help. The calculator returns the area in square meters. Notwithstanding this tin be automatically converted to other area units such equally foursquare feet or acres via the pull-down carte du jour:

Expanse based on radius:: A =`pi r^two`
Expanse based on diameter: A = `pi (d/two)^2`
Area based on circumference: A = `pi (c/(2pi))^2`
Surface area of a Sector (wedge, pie piece) based on radius (r) and angle (`theta`)
Area of Arc Segment given the radius (r) and angle (`theta`)
Area of Arc Segment given radius (r) and the depth (h) into the circle
Expanse of Circle Incribed inside a triangle given three sides (a,b,c) of the triangle
Area of Cirlce Circumscribing a triangle given three sides (a,b,c) of the triangle
Area of Annulus given the inner radius (r) and outer radius (R)

Notes

The surface area described in cerise in the commencement image on the left below is the area of the arc segment of of a circle. The expanse of the arc segment is defined by the angle `theta` and the circumvolve'south radius, r.

To find the expanse of the arc segment, we beginning find the expanse of the arc sector, shown in cherry-red in the 2nd image on the correct. This equations expanse is derived in the equation, "Circle -area of sector"

The simplified form of the formula for the expanse of the sector depends on whether the units used are degrees or radians.
)))

/attachments/452e1b50-9dd6-11e3-9cd9-bc764e2038f2/Arc sector - arc segment.png

The surface area of the segment can be seen graphically to be the difference between the area of the sector (defined by r and `theta` in the equation above) and the the area of the triangle defined by r and `theta` above -- or more properly the summation of the area of the 2 correct triangles with sides r, a, and b in the left picture.

Thus the area of one of the combined triangle whose center bending is `theta` is defined as ii * one/2 * base * 1/2 * height.

`"Area"_"triangle"` = two * (ane/2 * base * height)

= 2 * 1/2 * (r * sin(`theta`/ii)) * (r * cos(`theta`/ii))

= `r^ii` * sin(`theta`/2) * cos(`theta`/2)

Using the trigonometric identity sin(2u) = 2 sin(u) * cos(u) `=>` sin(u) * cos(u) = sin(2U)/2

we see sin(`theta`/2) * cos(`theta`/2) = `sin(theta)/2`

And so, `"Surface area"_"triangle"` = `r^two` * `sin(theta)/2`

And so `"Expanse"_"segment"` = `"Area"_"sector" - "Area"_"triangle"` where from the derivation of the surface area of a circle sector we have:

`"Area"_"Sector"`	`(theta` radians / `2pi " radians") * pi * r^2` = (`theta` / two) * `r^two`
	`(theta` degrees / `360 " degrees") * pi * r^two` = (`theta` / 360) * `pi *r^2`

So, for units given in radians, we have the \

`"Surface area"_"segment[radians]"`	((`theta` / two) * `r^ii`) - (`r^2` * `sin(theta)/2`)
`"Area"_"segment[degrees]"`	((`theta` / 360) * `pi * r^2`) - (`r^ii * sin(theta)/2`)